интерполация функции

Основните въпроси, разгледани в лекцията:

1. Основни понятия за интерполация, проблемът, водещи до сближаване на функции, геометрична смисъл на интерполация

2. Lagrange интерполация полином

3. Схема Aitken

4. оценка грешка Lagrange интерполация формула Един

5. крайни разлики

6. Newton интерполация формула

§ първия Newton интерполация формула

§ втори Newton интерполация формула

7. Оценка на първа и втора грешки Нютон интерполация формула

8. обратно интерполация

9. сплайн интерполация

1. Основни понятия на проблеми за интерполация, водещи до функцията за приближение

Интерполация (от латинската интерполация -. Вариант, промяна) - математика и статистика, определянето на стойността на междинни стойности за някои известни неговите стойности [SOV. Енциклопедичен речник].
Проблеми, които водят до сближаване на функции е както следва. Известни стойности на F функция (х) при X1 на точки. x2. Xn; което трябва да се възстанови стойността си в другия.
Интерполиране полином предаващите свойства на F функция (X) ще бъде изграден под формата:
Pn (х) = c1 # 966; 1 (х) + c2 # 966; 2 (х) +. + КН # 966 п (х), където # 966; 1 (х), # 966; 2 (х). # 966 п (х) - клас линейно независими функции, където Pn (XI) = F (XI), I = 1, 2. п.
По този начин, Pn (х) е (х).
Точка x1. x2. хп се наричат ​​интерполация точки.

· Lagrange интерполация полином

Да приемем, че стойността на F функция (X) в (п + 1) точка x0. x1. хп. Тогава Lagrange полином предаване свойства на F функция (X), могат да бъдат написани като:

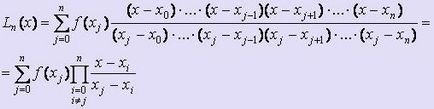
схема Aitken предлага по-удобна форма за намиране на Лагранж полином.
Основната идея на този метод е, както следва.
В първия етап се изчисляват полиноми L0,1 (х), L1,2 (х). LN-1, п (х), построена на всяка двойка от съседни възли 0.1; 1.2; :; п-1, п съответно.
В същото време. , ,
По този начин, полиноми са построени на две съседни възли са изчислени съгласно формулите.
След това, въз основа на тези полиноми се изчисляват полиноми конструирани по тройки на съседните възли :.
И т.н. докато не получи полином построен на всички възли на интерполацията :.
Получената полином L0, 1. п (х) Ln (х).

· Оценка за грешка Lagrange интерполация формула

Имаме YJ = F (XJ), Ln (х). Ln (х) полином е конструиран така, че LN (XJ) = F (XJ).
Изчисляване на грешката Rn (X), така че: Rn (х) = F (х) - Ln (х). Можете да получите следната формула за изчислената грешка на Лагранж интерполация формула:

.
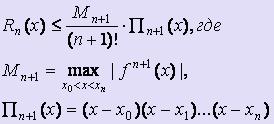
Такава оценка е възможно само, когато знаеш, аналитичната израз за ф. Ако е се определя в таблична форма, производните са заместени с крайни разлики.

· Newton интерполация формула

1. степента на полинома не надвишава н.

Формула Pn (х) за първи Newton интерполация формула е както следва :.
където Q = (х - x0) / час.
първо интерполация формула на Нютон се използва, ако х е началото на масата. Тогава, както и x0 трябва да се приема най-скоро ляво на дадена стойността на х табличен.

• втората Newton интерполация формула
  Когато стойност аргумент е по-близо до края на интервала на интерполация, нанесете първо интерполация формула става нерентабилно.
  За тази цел втората Newton интерполация формула.
  където Q = (х - х п) / час.
  Тук, както и х н трябва да вземат незабавно правото на дадена стойността на х табличен.

· Оценка на грешките от първия и втория Нютон интерполация формула

Използване на заместване р = (х - x0) / з и р = (х - х п) / ч и замествайки подходящо изразяване Pn + 1 (х) по погрешка формула оценка интерполация формула Lagrange, ние се получи формула за оценка на грешката за интерполация за първото и втората Newton интерполация формула, съответно:
.
.

Проблемът на обратен интерполация е както следва. Ако стойностите Yi> в таблицата са във възходящ ред или низходящ ред на функция у = F (х) е монотонна в [x0. хп] и съща маса може да се тълкува като определяне дискретен начин функция х = # 966; (у). обратна на функция у = F (х). За тази обратна функция може също да бъде натоварена интерполация: намиране на стойност х * от предварително определена стойност у *.

Нека XI> равноотдалечени възли, разположени на разстояние един от друг час и изградени от един от Нютон полиноми (за сигурност - първият).
При решаването на проблема с обратен интерполация използването на този полином в лявата му страна има известното стойността на у *. и самата формула става алгебрични уравнения по отношение на х. Ако номера у,> в възходящ или низходящ ред, това уравнение има уникално решение на [x0. хп].
Неговото решение трябва да се търси от някоя от по-рано изследваните методи за решаване на нелинейни уравнения.
В нашия случай, най-естественият начин за решаване на уравнението е просто повторение.
Ние заменен у = Y * в горната формула, и превръщане на получената уравнението на формата.
Това уравнение има структурата = х # 966; (х). т.е. от вид, подходящ за прилагане на метода на проста итерация.
Като начална приближение можем да вземем стойност х (0) = ХI. близо до желаната * х. С първоначална приблизителна х (0). Ние се изгради един повтарящ се процес за решаване на полученото уравнение, докато се достигне определеният точност:

С голям брой точки за интерполация силно градусови интерполиращите полиноми увеличава, което ги прави неудобни за изчисления.
В този случай е подходящо да се използва специален вид по части полином интерполация - сплайн интерполация.
Същността на този подход е, както следва.

Определение. Нека интервала [а, Ь] се разделя на п точки на частични сегменти [XI. XI + 1], I = 0, 1. N-1. функция М-за шлицов се нарича Sm (х). със следните свойства:
1) функция Sm (х) е непрекъсната върху интервала [а, б], заедно с техните производни до определен ред стр.
2) При всеки интервал [XI. XI + 1] функция съвпада с някои алгебрични mnogochlenomPm, и (х) на степен m.

Разликата от m - п между степента на най-висока степен на шпонката и непрекъснато върху интервала [а, Ь] се нарича производно дефект шпонката.
Ние считаме, шлици, дефект, който е един.

Най-широко използвани кубични сплайни S3 (х).

По този начин, за интерполиране шлицов необходимо да се конструира така, че S (XI) = ил. I = 0, 1. п.
По дефиниция, кубичен сплайн може да се запише като:

.
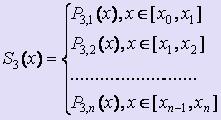
където всеки от Р 3, и (х) - трета степен полином :.
Коефициентите AI = ил.
Може да се покаже, че коефициентите на CI се изчислява чрез формулите :.
За да се изчисли коефициента на ди се използват формула.
За да се изчисли дву коефициенти - формула.