Свойства на умножението на естествените числа

Изхождайки от цялостното представяне на умножението на естествените числа. може да се отбележи редица резултати, специфични за тази дейност. Тези резултати се наричат ​​присъщите свойства на умножение на естествените числа. В тази статия ще ви покажем някои примери за основните свойства на умножение на естествени числа и да ги пиша с букви.

Навигация в страниците.

Комутативност на умножение на естествените числа.

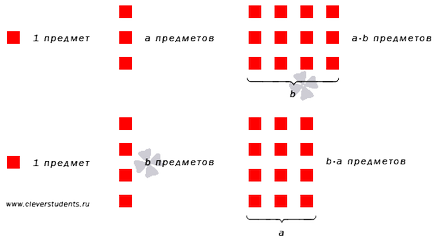
Размножаване на две цели числа има Комутативност. Ето текстът на имота: произведение на две числа не се променя, когато пермутация мултипликатори места. С писма от Комутативност на умножение могат да бъдат написани като: · б = б · а. където А и В могат да бъдат всякакви естествени числа (ако е необходимо, виж статията буквално експресия).

Вземем примера на потвърждаване валидността на Комутативност на умножение на две естествени числа. Въз основа на смисъла на умножение на две естествени числа. Ние изчисляваме продукта на числата 2 и 6, както и произведението от цифрите 6 и 2, и се уверете, че резултатите от умножение. Продуктът от цифрите 6 и 2, равен на сумата 6 + 6. от масата на добавяне е от 6 + 6 = 12. Продукт на числото 2 и 6 е сумата 2 + 2 + 2 + 2 + 2 + 2. който е равен на 12 (ако е необходимо, вижте материала на изделието и добавянето на още три числа). Следователно, 6 х 2 х 2 = 6.

Има схема, илюстрираща Комутативност на умножение на две естествени числа.

Асоциативност на умножението на естествените числа.

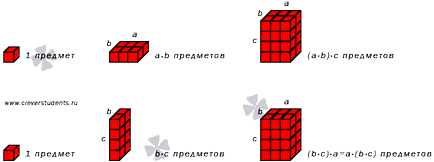
Наречен от асоциативен собственост на умножение на естествените числа: умножете това число чрез този продукт на две числа - е същото като това да умножите това число от първия фактор, а резултатът се умножи по Вторият фактор. Това означава, че · (б · в) = (а · б) · С. където. В и С могат да бъдат всякакви естествени числа (в скоби са затворени експресионни стойности се изчисляват на първо място).

Ето един пример, за да се потвърди асоциативните свойства на умножение на естествените числа. Изчисляване на продукта от 4 · (3 · 2). По смисъла на размножаването има 3 · 2 = 3 + 3 = 6. след 4 + (3 х 2) = 4 х 6 = 4 + 4 + 4 + 4 + 4 + 4 = 24. Сега извършва умножение (4 х 3) · 2. От 4 · 3 = 4 + 4 + 4 = 12. след това (3 · 4) = 12 · 2 · 2 = 12 + 12 = 24. Така, равенство 4 · (3 · 2) = (3 · 4) · 2. потвърждаване на валидността на въпросното имущество.

Ние показваме, която илюстрира асоциативност на умножението на естествените числа.

В заключение този раздел ние отбелязваме, че асоциативност на умножението може еднозначно да определи умножение на три или повече числа.

Разпределителни собственост на умножение над допълнение.

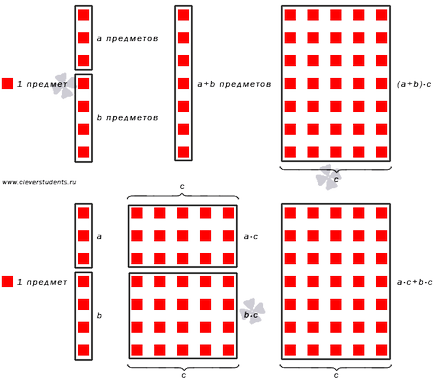
Следната собственост свързва събиране и умножение. Той е формулиран по следния начин: умножете тази сума на две числа в това число - това е едно и също нещо, както сгънатия продукт на първия срок и даденото число на произведението от втория мандат и броя. Този така наречен разпределително свойство на умножение над допълнение.

Ето един пример, потвърждаващ разпределителни собственост на умножение на естествените числа. Ние се провери валидността на уравнение (3 + 4) = 2 · 3 · 2 + 4 · 2. Имаме (3 + 4) * 2 = 7 х 2 = 7 + 7 = 14. и 3 · 2 + 4 · 2 = (3 + 3) + (4 + 4) = 6 + 8 = 14. следователно, уравнението (3 + 4) = 2 · 3 · 2 + 4 · 2 е вярно.

Ние претендираме модел, съответстващ на разпределителни собственост на умножение над допълнение.

Разпределителни собственост на умножение по отношение на изваждане.

Умножение и изваждане на естествените числа са свързани разпределителни собственост. Озвучен формулировка си: умножи тази разлика от два естествени числа, дадени за естествено число - е като тази на продукта и намаляване на броя на умалителят и изваждане на продукта от броя.

Използването на писма разпределително свойство на умножение по отношение на изваждането може да се запише като (а-б) · с = с · C-б · в. където. б и в - са естествени числа. По силата на Комутативност на умножение с формула също образуват · (В-С) = а · б-а · С.

Проверете валидността на свойствата на разпространение на умножение по отношение на примера на изваждане. Нека покажем, че равенството 3 * (4-2) = 3 · 4-3 · 2. Тъй 4-2 = 2 (ако е необходимо, се отнасят до теория раздел изваждане използва таблицата по допълнение), след това продуктът 3 · (4-2) е равна на произведението на 3 · 2. и 3 х 2 = 3 + 3 = 6. Нека сега да се изчисли разликата 3 · 4-3 · 2. Има 3 · 4-3 · 2 = (3 + 3 + 3 + 3) - (3 + 3) = 12-6 = 6. Така уравнение 3 * (4-2) = 3 · 4-3 · 2 полето.

единица собственост на умножение с естествено число.

Следващият Имотът е свързан с устройството за умножение и естествено число. По смисъла на умножение, продуктът на устройството и на естествено число п е равно на сумата от п условия, всеки от които е равна на едно. Следователно ,.

Например, продуктът от числата 1 и 37 е равно на 37; умножаване на резултата от 1 и 1004 е броят на 1,004.

На свой ред, продукт на п · 1 е лишена от смисъл (в смисъл на размножаването на тази работа е сумата на срок, равен на броя н. Добавяне но ние трябваше в продължение на две или повече думи). За да останем верни Комутативност на умножение, предполагаме, че е вярно равенството н · 1 = п.

Например, продуктът е равен на 298 и 1 298. и ако се умножи по 71 1. получаваме 71.

По този начин, продуктът от две положителни числа, един от които е равна на едно равно на друг номер. Последното твърдение е свойствата формулирането на умножение единици и естествено число. С помощта на този имот на умножение писма, написани като: 1 · п = п · 1 = п. където п - всяко цяло число.

Умножение собственост на нула до цяло число.

Въпреки нула не е просто число, но все пак за умножение собственост на нула и положително цяло число, ще разгледаме в тази статия. Това се дължи на факта, че този имот се използва в размножаването на природен номера колона.

Ако се придържаме към смисъла на умножение, продуктът 0 · п. където п - произволно число по-голямо от едно, п е сумата от условия, всеки от които е нула. По този начин. добавяне на имоти ни позволяват да се твърди, че последната сума е равна на нула.

За да се запази валидността на свойствата на умножение на естествените числа на устройството, които обсъдихме в предходния параграф, ще се счита за правилно следното уравнение 0 · 1 = 0.

По този начин, всеки естествено число п, равенството 0 · п = 0.

За да останем верни Комутативност на умножение да вземе равенство н · 0 = 0 за всяко естествено число п.

По този начин, продуктът от нула и положително цяло число, равно на нула. т.е. 0 · п = 0 и п = 0 · 0. където п - число. Последното твърдение е отчет за свойствата на умножение на естествените числа и нулата.

В заключение, ние представяме два примера, свързани с разбирам тази точка умножение собственост. Продуктът на числата 45 и 0 е нула. 0 Ако се умножи по 45 970. Фактът, също получаваме нула.

Вече спокойно можете да започнете да учите правилата, по които провеждат умножението на естествените числа.

• Математика. Всички учебници за 1, 2, 3, 4 класове на образователните институции.
• Математика. Всички уроци за 5 класа на образователните институции.