приемственост функция
Концепцията на непрекъсната функция математика дошъл, първи изучаване на различни закони на движение. Времето и пространството са безкрайно и зависимостта на, например, пътя и от време т. изразена право S = F (т). Тя дава пример за непрекъсната функция е (т). Промени непрекъснато, и температурата на нагрятата вода, също така е непрекъсната функция на времето: Т = F (т). Непрекъсната линия и, ако това може да се направи без повдигане молива от хартията. Тази линия е графика на непрекъсната функция.
Графично функцията е непрекъсната в точка, ако нейната графика не е "разбит" в този момент. Графика непрекъсната функция - е показано по-долу.
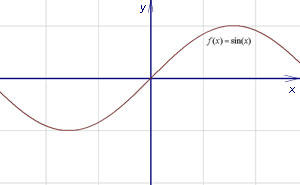
Определяне приемственост функция през граница. Функцията е непрекъсната в точката, при спазване на следните три условия:
1. Функцията дефинирани в точка.
2. Има ограничение функция в точка, дясно и ляво граници са равни.
3. граница функция в точка, равна на стойността на функцията в този момент:
Ако поне един от тези условия не е изпълнено, функцията не е непрекъсната в точката. В същото време се казва, че функцията е прекъсната, както и точките на графиката през които е прекъснато графика, наречени точки на прекъсване. Графиката на такава функция, потоци прекъсване на най х = 2 - долу.
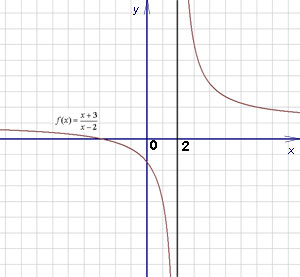
Пример 1. е (х) функция се определя, както следва:
Дали тази функция е непрекъсната във всяка една от граничните точки на неговите клонове, което е, в точките х = 0. х = 1. х = 3?
Решение. Проверяваме всички три условия непрекъснатост на функцията на всеки граничен пункт. Първото условие е изпълнено, тъй като тази функция се определя във всеки един от граничните пунктове, от дефиницията на функцията. Остава да се провери с другите две условия.
Точка х = 0. Ние считаме, лявата граница в този момент:
Намери ограничение на дясна:
Функцията граница и стойността на функцията в точката х = 0 трябва да се намери в клоновете на функцията, която включва тази точка, т.е. втората част. Намерете ги:
Както може да се види, и fuktsii гранична стойност на функцията при х = 0 са равни. Следователно, функцията е непрекъсната при х = 0.
Точка х = 1. Намираме граница от лявата страна в този момент:
Намери ограничение на дясна:
Функцията граница и стойността на функцията в точката х = 1, трябва да се намери в клоновете на функцията, която включва тази точка, т.е. втората част. Намерете ги:
Fuktsii граница и стойността на функцията при х = 1 е равна. Следователно, функцията е непрекъсната при х = 1.
Точка х = 3. Да се намери лявата граница в този момент:
Намери ограничение на дясна:
Функцията граница и стойността на функцията в точката х = 3, за да се намери в клоновете на функцията, която включва тази точка, т.е. втората част. Намерете ги:
Fuktsii граница и стойността на функцията при х = 3 са равни. Следователно, функцията е непрекъсната при х = 3.
По този начин, тази функция е непрекъсната при всяка граница точка.
Непрекъсната смяна на функция може да се определи като постепенната промяна, без скокове, където малка промяна малка промяна произтичат аргумент функция.
Нека илюстрираме тази постоянна промяна във функцията като пример.
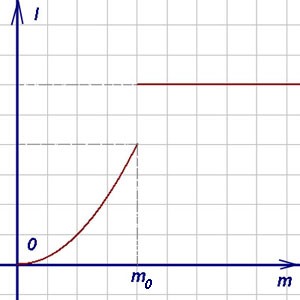
Нека по-горе виси на масата с товар нишка. Под въздействието на този товар резба се простира така, че разстоянието L от точка прежда натоварване суспензия е функция на натоварване маса м. т.е. л = F (т). m ≥0.
Ако промените малко маса на стоките, на разстояние L не се променя много. Така, малки промени m съответстват на малки промени л. Въпреки това, ако теглото на товара е в близост до крайната якост на преждата, малко увеличение в масата на товара може да причини резба счупване: разстояние L рязко увеличаване и става равна на разстоянието от точката на окачване на повърхността на масата. Графиката на L = F (т) е показана на Фиг. На тази графика парцела е непрекъснато (твърдо вещество) линия, и в точката беше спрян. Резултатът е графика, състояща се от двата клона. Всички точки с изключение на функция л = F (т) е непрекъсната и има при разкъсване на точка.
Изследване на непрекъснатостта може да бъде като независим задача, и един от етапите на пълно разследване на функцията и изграждането на своя график.
Непрекъснатостта на празнината. Нека функция у = F (X), определена от интервала] а. б [и непрекъснато във всяка точка на интервала. След това се казва, че е непрекъсната в интервал] а. б [. Подобно, понятието непрекъснатост се определя на интервалите на формата] - ∞, б [. ] А. + ∞ [. ] - ∞, + ∞ [. Да предположим, че след като функция у = F (X), определена за интервала [а. Ь]. Разликата между интервала и в интервала: интервал гранични точки не са включени в интервала, както и граничните точки на интервала са включени в сегмента. Тук трябва да споменем т.нар едностранно приемственост: точка А. Останалата върху интервала [а. Ь]. ние може да се обърне само правото и до точката B - само на ляво. Функцията се нарича непрекъснато върху интервала [а. Ь]. ако тя е непрекъснато на всички вътрешни точки този сегмент е непрекъснато в дясно и ляво непрекъснато в точка б.
Един пример за непрекъсната функция може да бъде всеки от елементарните функции. Всеки първоначален функция е непрекъсната по всяко интервал, в който е определена. Например, функциите са непрекъснати и във всеки интервал [а. Ь]. е непрекъсната върху интервала [0. Ь]. е непрекъснато на всеки интервал не съдържащ точка А на = 2.
Пример 2. За да се изследва функцията на непрекъснатост.
Решение. Проверяваме първото условие. Не е дефинирана функция в точките - 3 и 3. Най-малко едно от условията за непрекъснатост на цялата реална линия не се извършва. Ето защо, тази функция е непрекъсната на интервали
Пример 3. За да се определи при което стойността на параметъра през функция непрекъснат домейн
Решение.
Ние считаме, наляво граница функция на адрес:
Ние намираме граница дясната, когато:
Очевидно е, че стойността на мястото, х = 2 трябва да е равно на брадва: