Определен интеграл и методи на изчисление

Предишен ◈ Следващото

Определен интеграл на непрекъсната функция е (х) за ограничен интервал [а. Ь] (където) е увеличение на част от своята примитивен на този сегмент. (Всъщност, разбирайки много по-лесно ако се повтори тема неопределен интеграл) се използва този запис

Както е показано в долната диаграма (означен нарастване примитивна функция), определен неразделна може да бъде положителен или отрицателен номер (изчислено като разликата между стойността на примитивна в горната граница и е със стойност в долната граница, т. Е. Като F (б) - F (а)).

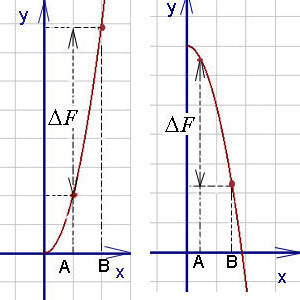
числа А и В се нарича долните и горните граници на интеграция, както и отсечката [а. Ь] - интервала на интеграция.

Така, ако F (х) - всеки примитив функция е (х), след това, по дефиниция,

Уравнение (38) е изразено от основните Нютон. разлика F (В) - F (а) се записва накратко, както следва:

Затова формулата на Нютон-Лайбниц ще бъде написан по този начин:

Ще докажем, че определеният интеграл не зависи от това дали примитивното на подинтегрален се взема, когато е оценен. Нека F (х) и F (х) - произволни примитиви подинтегрален. Тъй като това примитиви на същите функции, те ще се различава с постоянен срок: F (х) = F (х) + С. Следователно,

Това определя, че в интервала [а. Ь] инкрементира всички примитиви функция е (х) съвпадат.

По този начин, за да се изчисли определен интеграл е необходимо да се намери някакъв примитивен подинтегрален, т.е. първо трябва да намерите неопределен интеграл. Постоянният C на следващите изчисления изключено. Тогава основните теорема формулата се прилага: примитивна функция се заменя с горната граница на б. -нататък - ниска граница стойност и изчислява разлика F (б) - F (а). Полученият брой е определен интеграл.

Когато А = В, по дефиниция, взети

С цел да се практикува в намирането на определени интеграли нужда таблица на основните неопределени интеграли и ползи "Действия с правомощия и корени."

Пример 1. Изчислява определен интеграл

Решение. Първо трябва да намерите неопределен интеграл:

Прилагането на основните теорема на примитивен

(Когато C = 0), получаваме

Въпреки това, при изчисляване на определен интеграл е по-добре да не бъде в отделна примитивен и неразделна запис веднага във формата (39).

Проверете разтвора може да бъде в калкулатор линия на неопределени интеграли към получения изчисление примитивен заместител първа горна граница стойност и по-ниската пределна стойност и да намерят разликата. Полученият брой е определен интеграл.

Пример 2. Изчислява определен интеграл

Решение. като се използва формулата

Теорема 1.Opredelonny неразделна със същите граници на интеграция е нула. т.е.

Този имот се съдържа в дефиницията на определен интеграл. Въпреки това, той може да бъде получен чрез формулата на Нютон-Лайбниц:

Теорема 2.Velichina определен интеграл не зависи от предназначението на променливата на интеграция. т.е.

Нека F (х) - примитивна за F (х). За е (т) е примитивните на същата функция F (т), в която само независима променлива е посочено друго. Ето защо,

Въз основа на формула (39), последното равенство е равно интеграли

Теорема 3.Postoyanny фактор може да бъде взето в знак на определен интеграл. т.е.

Теорема 4.Opredelonny неразделна на алгебричната сума от краен брой функции, е равна на алгебричната сума на интегралите на някои от тези функции. т.е.

Теорема 5. Ако един сегмент на интеграция е разделен на части, а след определен интеграл в интервала равна на сумата на определени интеграли на неговите части. т.е. ако

Теорема 6. Когато пермутация интеграция ограничава абсолютната стойност на определен интеграл не се променя, а само променя своя знак. т.е.

Теорема 7 (теоремата на средната стойност). Определен интеграл е равна на произведението от дължината на интервала на интегриране на стойността на подинтегрален в някакъв момент в него. т.е.

Теорема 8. Ако горната граница на интеграцията и по-голяма от долната подинтегрален е неотрицателно (положително), а след това ф е неотрицателно определен интеграл (положително), т.е. ако

Теорема 9. Ако горната граница на интеграцията и по-голяма от долната и непрекъсната функция, тогава неравенството

Тя може да бъде интегриран план със срок. т.е.

Свойствата на определен интеграл ни позволяват да опрости директно изчисляване на интеграли.

Пример 3. Изчисляване на определен интеграл

Използване Теореми 3 и 4, и когато примитивите - таблични интеграли (7) и (6), получаваме

Нека е (х) - непрекъснато в интервала [а. Ь] функция, и F (х) - му примитивни. Помислете за определен интеграл

и от т означава променливата на интеграция, така че да не го бъркайте с горната граница. Ако х варира и промени opredolenny интегрални (47), т.е. тя е функция на горната граница на интеграция х. който е обозначен с F (х), т.е.

Ние се докаже, че функцията F (х) е примитивен за е (х) = F (т). Действително, диференциращ F (х), получаваме

функция F В (х) - един безкраен брой на примитиви за F (х), а именно това, което е най-х = а е нула. Това одобрение се получава, ако в (48) да се постави х = а и да се използва теорема 1 на предходния параграф.

В извличане формулата за интеграция чрез уравнение части ф DV = г се получава (UV) - об дю. интегрирането й в интервала от А до точка Б и като Теорема 4 параграф на тази статия за свойствата на определен интеграл, получаваме

Както следва от Теорема 2 раздел за свойствата на неопределен интеграл, първия мандат от дясната страна е равна на разлики в стойностите на UV на продукта най-горните и долните граници на интеграция. Писане тази разлика като за кратко

Ние се получи от части интеграция формула за изчисляване на определен интеграл:

Пример 4. Изчислява определен интеграл

Решение. Интегриране на части, като се има предвид и = LN х. DV = DX; след дю = (1 / х) DX. V = х. Чрез формула (49) намираме

Нека да преминем към изчисляване на определен интеграл от промяна на променлива. нека

където, по дефиниция, F (х) - примитивен за F (х). Ако променливата смяна в подинтегрален

в съответствие с формула (16) могат да бъдат написани

В този израз,

примитивна функция за

В действителност, негово производно, съгласно правилото за диференциране съставна функция е

Да предположим, че α и β - стойност на променливата Т. за които функцията

Тя счита, ценности А и Б. т.е.

Но, според формулата основните теорема, за разлика F (б) - F (а) е

Това е формулата за прехода към нова променлива под знака на определен интеграл. С него определен интеграл

след промяна на променливата

превръща в определен неразделна по отношение на нова променлива т. В този случай, старите граници на интеграция а и б са подменени с нови и извън него. , Трябва да се намери едно уравнение за нови ограничения

доставка стойности X = О и X = б. т.е. решава уравнения

и относително. След намирането на нови граници на изчисляването на интеграция на определен интеграл се свежда до използването на основните теорема на формула за интеграл от нова променлива тон. Примитивният функцията, която се получава в резултат на намирането на интегрална връщането към старата променливата не е необходимо.

При изчисляване на определен интеграл на метода на променлива замяна често е удобно да не изразя старата променлива като функция на новото, а по-скоро нова - като старата функция.

Пример 5. Изчислете определен интеграл

Решение. Proizvedom промяна на променлива, мислейки

След DT = 2x DX. където х DX = (1/2) DT. и подинтегрален се трансформира, както следва:

Намиране на нови граници на интеграция. Заместването на стойностите на х = 4 и х = 5 в уравнението

Сега с помощта на формулата (50), получаваме

След промяната на променлива, ние не се върне към старата променлива и се използва формулата на Нютон-Лайбниц към получения примитивното.

Започнете тема "Интеграл"

Предишен ◈ Следващото

Определен интеграл и методи на изчисление

Меню

Марка статии