Onnost функция

Монотонна функция - функция, която не се променя знака на стъпката, която е винаги неотрицателно или не-положителен винаги. Ако в допълнение на стъпката не е нула, тогава функцията се нарича строго монотонно. Монотонна функция - функция, която варира в същата посока.

Функцията се увеличава, ако по-голяма стойност на аргумента съответства на по-голяма стойност на функцията. Функция намалява ако голямата стойност на аргумента съответства на минимална стойност на функцията.

Нека функция на времето

функция се казва, че се увеличава от това дали

.

Функцията се нарича строго увеличаване на ако

.

Функцията се нарича намаляване на ако

.

Функцията се нарича строго намаляване на ако

.

(Строго) увеличаване или намаляване на функция се нарича (строго) и монотонно.

Функцията у = F (X) се нарича увеличаване (намаляване) на определен интервал, ако x1 F (х2)).

Ако диференцируема функция на у = е (х) в интервала [а, Ь] увеличава (намалява) негово производно в този интервал е '(х)> 0

Хо точка се нарича локален максимум (минимум) на F на функция (х), ако съществува квартал на Хо, за всички пунктове, където неравенството е (х) ≤ F (Ho) (е (х) ≥ F (Ho)).

Точка максимална и минимална екстремуми се наричат ​​точки, а стойностите на функцията в тези пунктове - неговите крайности.

Необходими условия за екстремум. Ако Хо е точка екстремум на F функция (х), след това или F '(Ho) = 0, или е (Ho) не съществува. Тези точки се наричат ​​критични и функцията се определя в критичната точка. Излага на функции, за да бъдат намерени сред своите критични точки.

Първото условие е достатъчно. Нека Хо - критична точка. Ако F '(х) при преминаване през точката Хо променя знак плюс минус, след това при точката функция Хо има максимален, в противен случай - поне. Ако минаваща през критичната точка на деривата не променя знак, а след това на мястото, Ho не екстремум.

Вторият достатъчно условие. Да предположим, че F функция (х) е производно F '(х) в съседство на Хо и втората производна на мястото Хо. Ако е "(Ho) = 0,> 0 (<0), то точка xоявляется точкой локального минимума (максимума) функции f(x). Если же=0, то нужно либо пользоваться первым достаточным условием, либо привлекать высшие производные.

На интервала [а, Ь] функцията Y = е (х) може да достигне до най-малкия или най-голямата стойност или критичните точки или сегменти в краищата [а, Ь].

7.Intervaly изпъкналост, интонация вдлъбнатина на топене.

Графиката на у = е (х) се казва, че е изпъкнала в интервала (а, Ь). ако е разположен по-ниско от някоя от нейните допирателна в този интервал.

Графиката на у = е (х) се нарича вдлъбната на интервала (а, Ь). ако тя е на всеки от своята допирателна в този интервал.

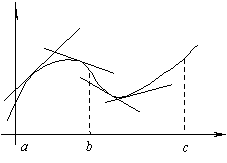
Фигурата показва кривата, изпъкнали на (а, б) и в вдлъбнат (б, с).

Полукръг изпъкнала в [1; 1].

парабола у = х2 вдлъбната на на интервала (-∞ + ∞).

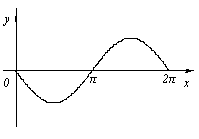
График функция в същите интервали може да бъде изпъкнала и вдлъбната друга. От графиката на у = грях х до [0,2; π], изпъкнала в интервала (0; π) и вдлъбнат (π; 2π).

Да разгледаме достатъчен критерий, който позволява да се определи дали графиката функция е в обхвата от изпъкнала или вдлъбната.

Теорема. Да предположим, че у = е (х) е диференцируема в (а, Ь). Ако всички точки на интервала (А; б) втората производна на функцията Y = е (х) е отрицателен, т.е. е '' (х) <0, то график функции на этом интервале выпуклый, если же f ''(x )> 0 - вдлъбната.

Доказателство. Предполагаме, за определеност, че е '' (х) <0 и докажем, что график функции будет выпуклым.

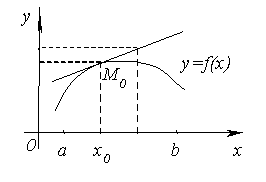
Разглеждане на графика функция у = F (х) на произволна точка с абсциса M0 x0  (а, б) и изготвя допирателна през точката M0. Нейната уравнение. Ние ще покаже, че графиката на функция (а, б) е под тази допирателна, т.е. в една и съща стойност х ординатата на крива Y = F (х) е по-малък от допирателната на ордината.

функция инфлексна точка

В този план, има и други приложения, вижте. Инфлексна точка.

точка определяне функцията инфлексия вътрешните tochkaoblasti като chtonepreryvna в този момент, има краен или безкраен производно определя характер на този етап, двата края iyavlyaetsya строг изпъкналост на интервала и началния интервал строг изпъкналост надолу, или обратно.

В този случай, yavlyaetsyatochkoy инфлексна точка на функцията на графиката, което означава, че графиката на функцията на "навежда" cherezkasatelnuyu да го в този момент: когато е допирателна под графиката и приори- горе графика (или обратно) на

Необходимо условие за наличието на точка на инфлексия, ако F функция (х), два пъти диференцируема в околност на точка на инфлексия е vtochku след това.

Достатъчно условие е наличието на точка на инфлексия, ако функцията в съседство tochkiraz непрекъснато диференцируема и prichemnechotno, и където един, funktsiyaimeet vtochku инфлексия.