Онлайн калкулатор - за изчисляване на определен интеграл (извитата част на трапеца)

Този математически калкулатор онлайн, за да ви помогне да се изчисли определен интеграл (площта на криволинеен трапец). Програма за изчисляване на определен интеграл (площ от криво трапец) не само дава отговор на проблема, той води до по-подробно обяснение решение. т.е. Тя показва процеса на интегриране на функцията.

То може да бъде полезно за студентите от висшите класове на средните училища в подготовка за тестове и изпити, проверка знанията преди изпита, на родителите да следят решенията на много математически и алгебра проблеми. Или може би са твърде скъпи за наемане на преподавател или да купят нови книги? Или просто искате възможно най-бързо, за да си напишат домашното по математика или алгебра? В този случай, можете да се възползвате от нашите програми с подробни решения.

По този начин можете да извършват своята част от обучение и / или обучение на малките си братя или сестри в същото ниво на образование в областта на задачите се увеличава.

защото готови за решаване на проблема много, вашата заявка се нарежда на опашка.
След няколко секунди, решението ще се появи по-долу.
Моля, изчакайте сек. Аз не искам да чакам!

Тези решения са създадени и съхранени от потребителите на нашия сървър
използването на този онлайн калкулатор.

В определеният интеграл.
Проблемите, довели до понятието определен интеграл

Задача 1 (за изчисляване на площта на криво трапец).

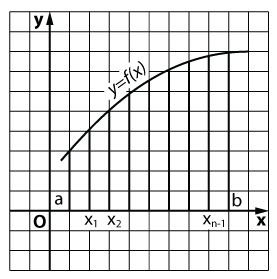
В Декартова координатна система XOY дадена фигура (вж. Фигура), ограничена от оста х, правите линии х = А, X = б (а

Концепцията на определен интеграл

Даваме математическо описание на модела, който е конструиран в три задачи считат за функция у = е (х), непрекъснато (но не задължително не-отрицателни, както се предполагаше, в проблемите считат) в интервала [а; Ь]:
1) разделяне на интервала [а; Ь] за п равни части;
2) е сумата

3) изчисляване

В хода на математически анализ доказа, че тази граница в случай на непрекъсната функция (или парче-мъдър непрекъснат) съществува. Това се нарича определен интеграл на функция у = е (х) за интервала [А; Ь] и е означена както следва:







Numbers а и б се наричат ​​границите на интеграция (съответно долна и горна).

Да се ​​върнем към проблемите, обсъдени по-горе. Определяне на зоната, представена в Задача 1 вече може да бъде пренаписана, както следва:

Тук S - площ на криво трапец е показано на фигурата по-горе. Това е геометрична смисъла на определен интеграл.

Определяне на преместване S на точка движи в права линия със скорост V = V (т), за интервал от време от Т = А до Т = Ь, дадени в Задача 2 може да бъде презаписано, както следва:

формула на Нютон - Лайбниц

За да започнете да отговори на въпроса: каква е връзката между определен интеграл и примитивното?

Отговорът може да бъде намерена в задача 2. От една страна, изместване S на точка движи в права линия със скорост V = V (т), интервала от време от т = до и т = б и се изчислява по формулата

От друга страна, точка на координатната се движи примитивен за скорост - означават си и (т); означава движението изразен с формулата S S = S (В) - и (а). В резултат на това, ние получаваме:

където S (Т) - примитивни за обем (т).

В хода на математически анализ доказва следната теорема.
Теорема. Ако функция у = F (х) е непрекъсната върху интервала [а; б], след това със следната формула

където F (х) - примитивен за F (х).

Горната формула обикновено се нарича Newton формула - Лайбниц след английски физик Isaaka Nyutona на (1643-1727) и немски философ Готфрид Лайбниц (1646- 1716), тя получи независимо и почти едновременно.

На практика, вместо на писане F (б) - F (а) се използва за влизане (понякога го наричат ​​двойна смяна), и съответно, пренапише Нютон формула - Лайбниц във формата:

Изчисляване на определен интеграл, първо намери примитивен, а след двойна смяна се извършва.

Въз основа на формулата на Нютон - Лайбниц, е възможно да се получат две свойства на определен интеграл.

Собственост 1. интеграл от сумата на функции е равна на сумата на интегралите:

Имоти 2. постоянен фактор може да бъде взето извън неразделна знака:

Изчисляване области на равнинни фигури посредством определени интеграли

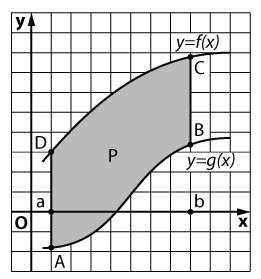
Използване на интеграл може да бъде изчислена площ е не само криволинейна трапец, но равнинни фигури по-сложна форма, като тази, показана на фиг. Фигура F ограничена от линии х = а и х = б и диаграми непрекъсната функция у = е (х), у = грам (х), където интервалът [а; Ь] неравенството. За изчисляване на площ S на фигурата, ще се процедира, както следва:

Така, формата на площ S, ограничена от линии х = а и х = б и графики функция у = е (х), у = грам (х), непрекъснато на интервала [а; Ь] и такова, че за всички х в интервала [а; Ь] неравенство се изчислява по формулата

Таблица неопределени интеграли (примитиви) на определени функции

$$ \ Int 0 \ cdot DX = C $$

$$ \ междинно съединение 1 \ cdot DX = х + C $$