непрекъснатост

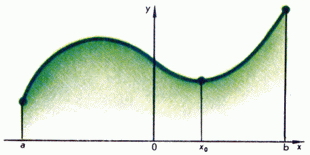
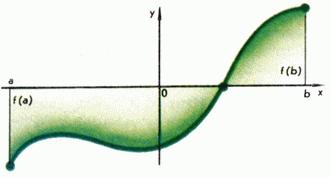
Да разгледаме две функции, чиято графики са показани на Фиг. 1 и 2. графиката на първата функция може да се направи без повдигане молива от хартията. Тази функция може да се нарече непрекъснато. График друга функция, така че е невъзможно да се направи. Състои се от две непрекъснати парчета и има разлика в точката, и ние наричаме функцията за избухване.

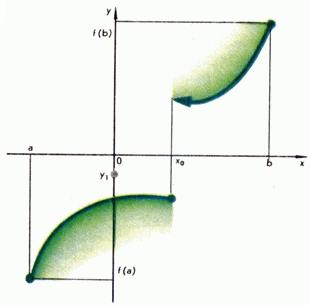
Такава ясна дефиниция на приемственост не може да се организира по математика, тъй като тя съдържа напълно не-математическа концепция за "молив" и "на хартия". Точното математическо определение на приемственост се дава въз основа на концепцията за граница и е както следва.

Нека функцията е определено по-интервала и - точка на този сегмент. Функцията се нарича непрекъснато в точката, ако упражняването (наблюдавани само в интервала) стойности са склонни да функционира, т.е. ако

Функцията се нарича непрекъсната в интервала, ако тя е непрекъсната във всяка точка.

Ако точката на уравнението (1) не е изпълнено, функцията се нарича прекъсната в точката.

Както се вижда, непрекъснатостта на математическа функция на интервала се определя от местното (местно) непрекъснатост на точката.

Стойността се нарича увеличение на аргумента, функцията разлика е функция стойностите на прираста и се означава. Очевидно е, че като аргумент за нарастването клони към нула :.

Нека да пренапише уравнение (1) в еквивалент под формата

С помощта на тази бройна система, тя може да бъде пренаписана, като:

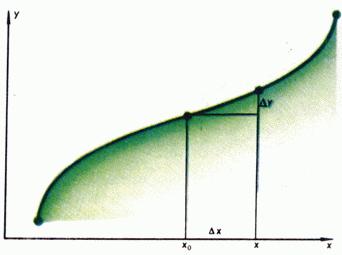
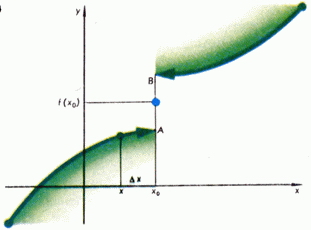
Така че, ако функцията е непрекъсната, а след това на аргумента клони към нула нарастване нарастване на функцията клони към нула. Говорете по различен начин: една малка увеличение на аргумента съответства на слабо увеличение на функцията. Фиг. 3 е графика на непрекъсната функция в точката, увеличението съответства на функция за увеличение. Фиг. 4 увеличение съответства на вариант на функцията, която, колкото и малка да е, няма да е по-малко от половината от дължината на сегмента; функция е прекъснат в точката.

Нашата идея на непрекъсната функция като функция, която може да се направи графика без повдигане молива от хартията, както се поддържа от свойствата на непрекъснатост, които могат да бъдат доказани в математически анализ. Имайте предвид, например, такива свойства.

1. Ако непрекъснат сегмент на функцията се в краищата на стойностите на сегмента на различни признаци, след това в някакъв момент от този интервал е необходимо стойността на нула.

2. Функцията е непрекъсната върху интервала, получава всички междинни стойности между стойностите на крайните точки, т.е. между и.

3. Ако функцията е непрекъсната в интервал, а след това в този интервал тя достига своя максимум и минимална стойност, т.е. ако - най-малкият и - най-голямата стойност на функцията на интервал, тогава има точки на този сегмент и това.

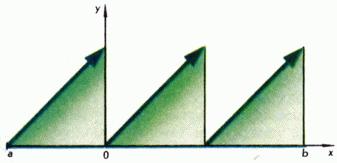
Геометричната смисъла на първата от тези отчети е доста ясна: ако непрекъсната крива преминава от едната страна до другата ос, той пресича тази ос (Фигура 5.). Прекъснати функция има това свойство, както се вижда от графиката на фиг. 2, както и на свойствата на 2 и 3. На фиг. 2, функцията не приема стойността, въпреки че той се намира между и. Фиг. 6 показва пример за прекъснат функция (фракционна част), която достига максималната си стойност.

Един пример за непрекъсната функция може да бъде всеки от елементарните функции. Всеки първоначален функция е непрекъсната по всяко интервал, в който е определена. Например, функциите са непрекъснати и във всеки интервал, интервалът е непрекъсната, непрекъсната функция на всеки интервал не съдържащ точка.

Събиране, изваждане, умножение непрекъснато върху същите функции сегмент отново да доведе до непрекъснатост. Когато се раздели на две непрекъснатост ще бъде непрекъсната функция, ако знаменателят е различна от нула навсякъде.

Концепцията на непрекъсната функция математика дошъл, първи изучаване на различни закони на движение. Пространството и времето са непрекъснати и зависимост, например, по пътя от време на време, изразено от закона, е пример за непрекъсната функция.

С непрекъснатост описват състояния и процеси в твърди вещества, течности и газове. Студентите на науката - Теория на еластичността, хидродинамика и аеродинамика - са обединени от едно име - "Continuum Механика".