Непрекъснато функция 1
Непрекъсната функция - един от основните понятия на математическия анализ. Непрекъснати функции са много по-чести, отколкото диференцируема. множеството от всички непрекъснатост е затворен при аритметични операции (с изключение на участък) и състава и форми, ако не е най-важен клас функции в анализа. Въпреки това, строга математическа дефиниция на непрекъсната функция, Коши собственост - е сравнително нова и изисква високо ниво на математическа абстракция. Интуитивно същото определение е: непрекъсната функция на реална променлива, ако малки промени в аргумента съответства на малки промени в стойността на функцията могат да бъдат написани както следва: където Това означава, че графиката на непрекъсната функция все още няма прекъсвания, т.е. Това може да се проследи ", без да вдигате молива от хартията." Всички елементарни функции - непрекъснати по своя домейн.
1. Определение
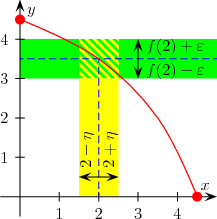
Пример непрекъсната функция
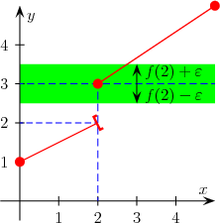
Пример за прекъснат функция в точка. Функцията не е непрекъсната от левия точка
но тя е непрекъсната в дясно:
2> е (х) = 3 = F (2) "SRC = / изображения / ukbase_1_807531046_1006.jpg />.
Функцията на една реална променлива, дадена в областта. Непрекъснато в произволна ако 0 "SRC = / снимки / ukbase_1_807536710_299.jpg /> 0, съществува" SRC = / снимки / ukbase_1_807537385_320.jpg /> (което зависи от), която трябва да бъде непрекъсната функция в района. Ако е непрекъсната във всяка точка на този домейн.
Да. - ограничение точка А.
1.1. Определяне на непрекъснатост в точка
F Функцията е непрекъсната в точка, ако:
- F функция (X), определена в точка х 0.
- има ограничение
- .
1.2. Определяне на непрекъснатост в точката на Коши
F Функцията е непрекъсната в точка, ако: 0) "SRC = / изображения / ukbase_1_807552570_496.jpg /> 0) \ forall х" SRC = / изображения / ukbase_1_807553627_612.jpg />. Какво =>
1.3. Определяне на непрекъснатост в точката на Хайне
F Функцията е непрекъсната в точка, ако :. Ако. Това.
2. Поставете точки
брейк пойнт - това е точка (стойност на аргумента), където функцията не е непрекъсната.
Следните видове точки на прекъсване:
Скъсване нарича прибиращ се, ако в този момент има ограничение функция не съвпада с функцията стойност.
Точка от първи вид се нарича точка на прекъсване, ако има крайни леви и десни граници на дадена точка, и те не съвпадат.
Ако поне един двустранен граница не съществува, безкрайността, точката се нарича брейк пойнт от втори ред.