Монотонни функции - studopediya

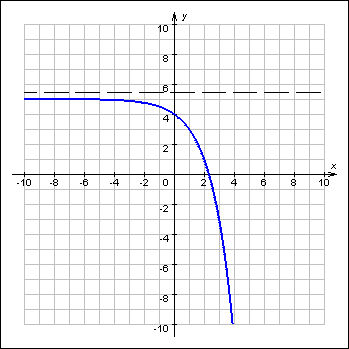
Фигура 1.3.5.1. Интервали от увеличаване и намаляване функция

В графиката, показана на фигура функция у = е (х), се увеличава на всеки от интервалите [а; х1) и (х2; Ь] и намалява разликата (х1, х2). Забележете, че увеличава функция при всеки от интервалите [а; х1) и (х2; Ь], но не и на интервали интеграция

Ако функцията се увеличава или намалява по някакъв интервал, а след това той се нарича монотонно на този интервал.

Забележете, че ако е - монотонна функция на интервал г (е (х)), тогава F уравнение (х) = конст може да има повече от един корен в този интервал.

В действителност, ако x1

Ние списък на свойствата на монотонни функции (предполага се, че всички функции, определени в определен интервал D).

• Сумата от няколко увеличават функции е нарастваща функция.
• Произведение неотрицателно нарастваща функция е нарастваща функция.
• Ако функция F се увеличава, след това функции CF (C> 0) и е + C също се увеличава, и CF на функция (в <0) убывает. Здесь c – некоторая константа.
• Ако F увеличава и запазва своя знак, функцията 1 / F намалява.
• Ако функция F се увеличава и не е отрицателен, тогава къде. също се увеличава.
• Ако F увеличава и п - нечетно число, а след това Fn също се увеличава.
• Състав г (е (х)) увеличаване функции е и ж също се увеличава.

Подобни изявления могат да бъдат формулирани за намаляване функция.

Модел 1.9. свойства на функцията

точка се нарича максимум на функцията F. ако има # 949; околност на. че неравенството е (а) ≥ е (х) за всеки х от този район.

точка нарича точка на минимум на функцията F. ако има # 949; околност на. че за всички х в тази съседство на неравенство F (а) ≤ е (х).

Точката, в която максимално или минимално на функция, наречена екстремумът точки.

Целта на екстремум е промяна на характера на монотонност. Така че, в ляво от точката на екстремалната функция може да се увеличи, както и правото - да се намали. По дефиниция, точката на екстремални трябва да е точка вътре в домейна.

Ако по някаква (х ≠ а) неравенството е (х) ≤ е (а), тогава точката се нарича точка на максималните стойности на набор D:

Ако по някаква (х ≠ б) неравенството е (х)> е (б) на точка В е точка на най-малката стойност на комплекта D.

най-високите или най-ниските стойности на една точка може да бъде функция екстремум, но не е задължително да е то.

Най-висока точка (малката) стойност на непрекъсната функция в интервала да се намира между екстремумите на тази функция и нейните стойности в крайните точки.