монотонна функция

Монотонна функция - функция, която не се променя знака на нарастване, което е било винаги отрицателно или винаги положителен. Ако в допълнение на стъпката не е нула, тогава функцията се нарича строго монотонно. Монотонна функция - функция, която варира в същата посока.

Функцията се увеличава, ако по-голяма стойност на аргумента съответства на по-голяма стойност на функцията. • функция намалява, ако по-голямата стойност на аргумента съответства на минималната стойност на функцията.

условията за монотонност:

(Критерий монотонност на като производното в интервала) Да

непрекъснато на (а, Ь), и има при всяка точка

производно F '(х). след това

F увеличава с (а, Ь), ако и само ако

е намалява на (а, Ь), ако и само ако

Достатъчно условие за друга монотонна функция има производно в интервала) Да

непрекъснато на (а, Ь), и има при всяка

производно F '(х). след това

след това е строго увеличаване на (а, Ь);

след това е строго намаляване на (а, Ь).

Обратното не е вярно по принцип. Производното е строго монотонно функция може да изчезне. Въпреки това, множеството от точки, където производното не е нула, трябва да бъде плътно върху интервала (а, Ь). По-точно държи

(Критерий за стриктно монотонност на като производното в интервала) Да

и навсякъде в производно F '(X). След това е строго увеличаване на интервала (а, Ь), ако и само ако са изпълнени следните две условия:

По същия начин, е строго намаляване на интервала (а, Ь), ако и само ако са изпълнени следните две условия:

24. екстремум функции. Необходимо условие за екстремум (теорема на Ферма). Достатъчен състояние на екстремум.

Достатъчно условие за увеличаване (намаляване) функция на интервала. Концепцията за екстремни функции. Необходимо условие за екстремум на функция (теорема на Ферма).

Ако производното е непрекъсната функция е (х) е положителен, в определен интервал (F '(х)> 0), тогава тази функция се увеличава интервал.

Ако производното е непрекъсната функция е (х) е отрицателен в някакъв интервал (F '(х)<0), то на этом промежутке функция убывает.

Тези условия са достатъчни условия за увеличение (намаление функция).

Ние ще се опитаме да разберем защо това се случва (строга доказателство се вижда в програмата на висшите учебни заведения). Известно е, че геометричната смисъла на производното - наклона на допирателната. Следователно, ако производното е положителен, ъгълът е остър.

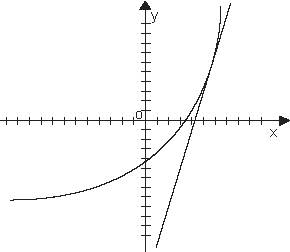
И се оказва, че графикът е "нагоре по хълма". Ако производното е отрицателен, ъгълът на наклон е тъп, се оказва, че графиката е "надолу".

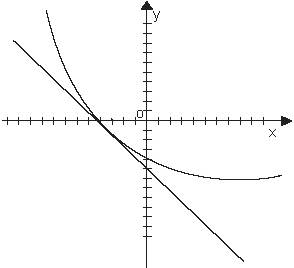
Интервали от нарастване и спад пропуски наречени монотонни.

Точка x0 е точка на максималната функция F (х), ако съществува положително число Е, така че за всяко х в интервала

С други думи, F функцията стойност (x0) е най-големият в квартал на x0.

Точка x0 е точка на минимум F функция (х), ако съществува положително число Е, така че за всяко х в интервала

С други думи, F функцията стойност (x0) е най-малкият в квартал на x0.

Следната таблица точка -9 и 3 точки на максимална и точката -2 е минимална точка.

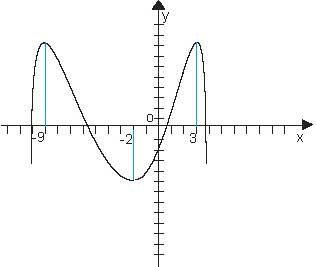
Точка на максимални или минимални точки се наричат ​​крайност.

теорема на Ферма: Ако x0 - екстремум точка непрекъсната функция е (х), след това е "(x0) = 0.

Геометрично, изглежда така: в екстремум допирателната успоредна на говедото на ос и, следователно, ъгълът на наклон е 0.

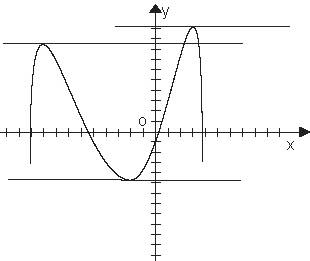
Това условие е необходимо, но не достатъчно условие за екстремум.