Концепцията за непрекъснатост на

Определение. е (х) функция. дефинирана в околност на. и го нарича непрекъсната в точката. ако (1)

Така, функцията F е непрекъсната при. ако са изпълнени следните условия:

1. F Функцията се определя в съседство на. т.е. има редица така, че U;

непрекъснатост Определяне функция е (х) на. изразена от състояние (1) могат да бъдат формулирани с помощта на (в език), и използване на околната среда по отношение на последователности, съответно

Ще подчертая, че определението за непрекъснатост, за разлика от определението на срока се счита за завършена, и не е пробита квартал на една точка. и границата на функцията е стойността на функцията в точка а.

Ние наричаме х разликата - едно увеличение на аргумента и нека х. и F на разлика (X) - е (а) - функцията за увеличение. съответстващ на даден нарастване на аргумент х. и нека у. По този начин,

х = х - а, у = е (х) - е (а) = F (а + х) - е (а).

С тази нотация уравнение (1) е под формата

Така продължителността на точка означава, че безкрайно увеличение на аргумента съответства на функция безкрайно увеличение.

По аналогия с концепцията на срока на ляво (вдясно) представи концепцията за непрекъснатост на ляво (вдясно). Ако функция F се определя на интервала и. t.e.f (а - 0) = F (а). След това тази функция се нарича ляв непрекъснато в.

По същия начин, ако функцията F се определя на интервала, и F (а + 0) = F (а). След това тази функция се нарича прав непрекъснато в.

Например, F функция (х) = [х] е непрекъсната полето до точката х = 1, и не е непрекъсната отляво в този момент, тъй F (0 - 1) = 0, F (1 + 0) = F (1) = 1.

Очевидно е, че функцията е непрекъсната в този момент, ако и само ако това е непрекъснат, както наляво и надясно в този момент.

В стъпка 2, предполагаме, че функцията е определена в квартал на спукан.

Точка се нарича точка на прекъсване функция е. ако тази функция е или не е определено по-, или е определен, но не е постоянен в.

Следователно, и - точка на прекъсване на ф. ако не се извършват най-малко един от следните условия:

2) има ограничен

Ако добре - функция буква е почивка, и в този момент там са ограничени граници на ляво и на дясно, т.е. точката се нарича брейк пойнт от първи ред.

Едностранно приемственост. Класификация точки на прекъсване.

5.4.1. Определяне едностранно приемственост.

При определяне на непрекъснатостта на функцията на x0 изисква съществуването и равенство. С прилагането на едностранни граници се определят с понятието непрекъснатост на функция в ляво и дясно:

Opr.5.1.7. е (х) функция се нарича непрекъснато в точка x0 отляво ако.

Opr.5.1.8. е (х) функция се нарича непрекъснато в x0 полето, ако.

F функцията (х) се нарича непрекъснато върху интервала [а. Ь], ако е непрекъснато на интервала (а. б), е непрекъсната в дясно и ляво непрекъснато в точка б.

Забележка. Функцията е непрекъсната върху интервала [а, Ь] може да бъде прекъснат в точки А и В (фиг. 1)

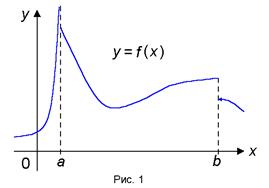
Наборът от функции, които са непрекъснато в интервала [а. Ь] е обозначен с С [а. Ь].

Свойства на функции непрекъснати върху интервала

Теорема 1 (обем ограничен непрекъсната функция). Ако F функция (х) е непрекъсната върху интервала [а. Ь], е ограничен до този интервал, т.е. съществува номер C> 0 и "х Î [A. Ь] неравенството | F (X) | ≤ В.

Теорема 2 (Вайерщрас). Ако F функция (х) е непрекъсната върху интервала [а. б], след това да достигне този сегмент от максималната му стойност М и минимум m стойност. т.е. има точки # 945;. # 946; Î [A. Ь] така, че m = F (# 945) ≤ е (х) ≤ F (# 946) = М за всички х Î [A. Ь] (Фигура 2).

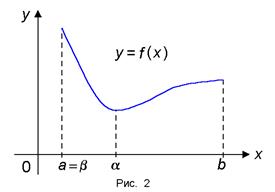
Теорема 3 (съществуването на нула). Ако F функция (х) е непрекъсната върху интервала [а. (. а б) б] и в крайните точки се ненулеви стойности на различни признаци, след интервала съществува поне една точкова # 958; където F (# 958) = 0.

Геометричната смисъла на теоремата е, че графиката на функция отговаря на условията на теоремата, задължително да премине ос вола (Фигура 3).

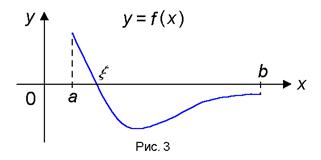
Забележка. На тази теорема базиран метод за приблизителното решението на уравнението