Калкулатор онлайн - решения логаритмични уравнения

Този математически калкулатор онлайн, за да Ви помогне да решите логаритмична уравнение. Програма за решаване на логаритмични уравнения не просто да даде отговор на проблема, той води до по-подробно обяснение решение. т.е. Тя показва процеса на получаване на отговор.

То може да бъде полезно за студентите от висшите класове на средните училища в подготовка за тестове и изпити, проверка знанията преди изпита, на родителите да следят решенията на много математически и алгебра проблеми. Или може би са твърде скъпи за наемане на преподавател или да купят нови книги? Или просто искате възможно най-бързо, за да си напишат домашното по математика или алгебра? В този случай, можете да се възползвате от нашите програми с подробни решения.

По този начин можете да извършват своята част от обучение и / или обучение на малките си братя или сестри в същото ниво на образование в областта на задачите се увеличава.

влизане (б) или вход (д, б) - натуралния логаритъм на б
влезте (10, б) - десетичен логаритъм на б
влезте (а, б) - на логаритъм от б до база

защото готови за решаване на проблема много, вашата заявка се нарежда на опашка.
След няколко секунди, решението ще се появи по-долу.
Моля, изчакайте сек. Аз не искам да чакам!

Тези решения са създадени и съхранени от потребителите на нашия сървър
използването на този онлайн калкулатор.

Логаритмична функция. логаритми

Задача 1. Виж положителния корена на уравнението х 4 = 81
По дефиниция имаме корен аритметика \ (х = \ SQRT [4] = 3 \)

Задача 2. решаване на уравнението 81 х = 3
Пишем уравнението, както следва: х = 3 4. 3, където х = 4

В задача 1 е неизвестен база степен, както и проблем 2 - показател. 2 начина на решаване на проблема е, че от лявата и дясната страна на уравнението може да бъде представен като степен с една и съща база 3. Но, например, уравнението 3 х = 80 по този начин не е възможно да го реши. Все пак, това уравнение има корен. За да може да разреши тези уравнения, ще се въведе концепцията за логаритъм от броя.
Уравнение х = б, където> 0, \ (а \ НЕК 1 \), б> 0, има уникален корен. Този корен се нарича логаритъм на б не база и определено Лога б
Например, корена на уравнението 81 х = 3 е броят 4, т.е. log3 4 = 81.

Определение. Логаритъм на положително число в база б а, когато> 0, \ (а \ НЕК 1 \) се нарича експонат, който искате да се повиши броят на, за да получите б

log2 8 = 3, защото 2 3 = 8

log7 7 = 1, от 7 = 7 1

Определяне на логаритъм може да се запише като:

Това уравнение е валидно за б> 0, б> 0, \ (а \ НЕК 1 \). Той обикновено се нарича основната логаритмична идентичност.

Действието на намирането на логаритъм от броя нарича логаритмите.
Действието на определяне на броя на логаритъм, се нарича потенциране.

Изчислете log64 128
Нека х = log64 128. По дефиниция, 64 логаритъм от х = 128. От 64 = 2 6. 128 = 2 7. 2 на 6Х = 7. 2 от 6x = 7, х = 7/6.
Отговор log64 128 = 7/6

Изчислява \ (^ 3 \)
Използване на свойствата и степента на основния логаритмична идентичност, ние откриваме

Решаване на уравнение log3 (1-х) = 2
Чрез логаритъм определение 2 март = 1 - х, където х = -8

Свойствата на логаритми

Когато трансформациите на изразяване, съдържащи логаритми, в изчисленията и уравненията за решаване на различни свойства често се използват логаритми. Помислете за основните от тях.

Да предположим, че е> 0, \ (а \ НЕК 1 \), б> 0, с> 0, R - всяко реално число. След това по следната формула:

2) \ (\ log_a \ Frac = \ log_a б - \ log_a С \)

Десетични и натурални логаритми

За логаритми от числа, изготвен специални таблици (таблици на логаритми). Логаритми, изчислена по калкулатора. В този и в другия случай са само знака след десетичната или натурални логаритми.

Определение. Десетична логаритъм от броя се нарича логаритъм от броя на база-10 и писмен
LG б вместо log10 б

Определение. Натуралния логаритъм на броя нарича логаритъм от броя на база д, където д - ирационално число, приблизително равна на 2.7. Когато този запис LN б вместо Loge б

Ирационално число д играе важна роля в областта на математиката и нейните приложения. Броят д може да се представи като сума от:
$$ е = 1 + \ Frac + \ Frac + \ Frac + \ точки + \ Frac + \ точки $$

$$ д \ около 2,7182818284 $$

Оказва се, че е достатъчно да се знае само десетичната стойност или само натуралните логаритми на номера, за да намерите най-логаритмите на номера по някаква причина.
За тази цел замяна на логаритъм база формула:

където В> 0, а> 0, \ (а \ НЕК 1 \), с> 0, \ (в \ НЕК 1 \)

Последици от формула замяна логаритъм основа.
Ако с = 10 и с = е получен чрез преход Формула да е десетична логаритми и естествено:
$$ \ log_a б = \ Frac. \; \; \ Log_a б = \ Frac $$

Логаритмична функция, неговите свойства и графика

В математиката и нейните приложения общ логаритмична функция
у = Loga х
и където - предварително определения брой, а> 0, \ (а \ НЕК 1 \)

В логаритмична функция има следните свойства:
1) домен на логаритмичната функция - множеството от всички положителни числа.

2) зададените стойности на логаритмична функция - множеството на всички реални числа.

3) логаритмична функция не е ограничен.

4) логаритмична функция у = Loga х е за увеличаване на интервал \ на ((0 + \ infty) \), ако> 1,
и намаляване, ако 0 1, след това функция у = Loga х отнема положителни стойности за х> 1,
отрицателни за 0 1.

Oy ос е вертикална асимптота на графиката на у = Loga х

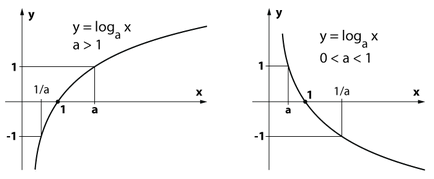
Имайте предвид, че всяка графика на логаритмичната функция Y = Loga х преминава през точката (1; 0).
В решаването на уравнения често се използва следната теорема:

логаритмична функция у = Loga х и експоненциалната функция Y = а х. където> 0, \ (а \ НЕК 1 \) са взаимно обратен.

логаритмични уравнения

Решаване на уравнение log2 (х + 1) + log2 (х + 3) = 3
Да приемем, че х - е число, при която равенство е вярно, т.е. х - корена на уравнението. След това, от имуществото на логаритъм от равенството
log2 ((х + 1) (х + 3)) = 3
От това уравнение за определяне на логаритъм получаваме
(X + 1) (х + 3) = 8
х 2 + 3 + 4 = 8, т.е. х 2 + 4x - 5 = 0, X 1 = 1, х2 = -5
Тъй като квадратно уравнение е следствие от оригиналната формула, е необходимо да се провери.
Провери дали числата 1 -5 и корените на първоначалното уравнение.
Заместването на лявата страна на първоначалното уравнение х = 1, получаваме
log2 (1 + 1) + log2 (1 + 3) = log2 2 + log2 4 = 1 + 2 = 3, т.е. х = 1 - корена на уравнението.
Когато х = -5 + 1 номер х + 3 и х е отрицателна, и следователно от лявата страна на уравнението няма смисъл, т.е. = -5 х не е корен на това уравнение.
Отговорът е х = 1

Lg решаване на уравнение (2x 2 - 4x + 12) = х + LG LG (х + 3)
Чрез собственост на логаритми
LG (2х 2 - 4x + 12) = LG (х 2 + 3 х)
Дето
2 2х - 4x + 12 = х 2 + 3x
х 2 - 7х + 12 = 0
X1 = 3, Х2 = 4
Тестване показва, че двете стойности на х са корените на първоначалното уравнение.
x1 Response = 3, Х2 = 4

Решаване на уравнение log4 (2х - 1) • log4 х = 2 log4 (2х - 1)
Нека да превърне това уравнение:
log4 (2х - 1) • log4 х - 2 log4 (2х - 1) = 0
log4 (2х - 1) • (log4 х - 2) = 0
Приравняването на всеки фактор в лявата част на уравнението на нула, получаваме:
1) log4 (1 - 2) = 0, където 1 - 2 = 1, Х1 = 1
2) log4 х2 = 0, където log4 = 2, Х2 = 16
Тестване показва, че двете стойности на х са корените на първоначалното уравнение.
Отговор x1 = 1, х2 = 16

Книги (книги) Книги (други) Резюмета изпит и OGE тества онлайн игри, пъзели заговор функции речник на младостта жаргон каталог Училища България Каталог SSUZov България Каталог България университети проблеми с намирането на НОД и НОК Опростяване полином (полином умножение) полином дивизия от полином колона Изчисление числени фракции решаване на проблеми в проценти комплексни числа: сума, разлика, продукти и коефициент системи 2 линейни уравнения с две променливи разтвор на квадратно уравнение удебелен квадратен г vuchlena и факторинг квадратичен полином неравенства решения неравенства решения диаграми система квадратна функция Графики линеен фракционна функция решаване аритметика и геометрична прогресия решение тригонометрични, експоненциални, логаритмични уравнения Изчисляване на граници, производно, допирателни интегрални примитивни разтвор триъгълници Изчисления действия с вектори Изчисленията линия на действие и размер равнина на геометрични форми геометрична фигура периметра площ обем повърхност на геометрични форми геометрични форми
Дизайнер ситуации на пътя
Времето - Новини - хороскопи
MathSolution.ru програма на Google Play