Какво е ЕБФ
3.3.Temperaturnoe поле на постоянен неподвижна точка източник-Ni-ка в безкраен среда. Гаус функция грешка (ЕБФ (х)).
Ако точка KE с координати х ". Y '. Z 'в интервала от време от т' = 0 до т '= т ра-бота източник топлинна енергия W, полето за температура на IP-точка-аудио-ка, както е дефинирано по-горе, п-Jette да се намери чрез интегриране на основен разтвор на т' от 0 до т (тоест, от захранването до изключване). Намерете произхода на координати на мястото, където източникът тъпка ла. След X '= Y' = Z '= 0, и формулата за температурата става:
Ние направи неразделна (3.3.1) промяната на променливи r2 / [4а (т - т ')] = 2. След това: (т - т ") 3/2 = R3 / (8a3 / 23), DT '= r2d / (2a3). границите на интеграция: т "= 0
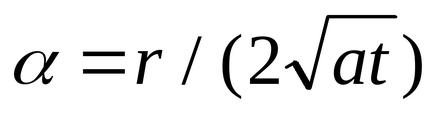
Първият интеграл в скобите, е известно от курса на висша математика:
а вторият интеграл от гледна точка на елементарни функции не може да се изрази и определя специален удоволствие от ТА, който се нарича на Гаус грешки функция. или интеграл на вероятностите. или забавно за хи-тя erfektum:
(Прочетена "erfektum" или съкращението "ORF"). Чрез тази функция на разтвора, изразена чрез поставените-много проблеми в теорията на топлопроводимост, и в други области на физиката играе важна роля.
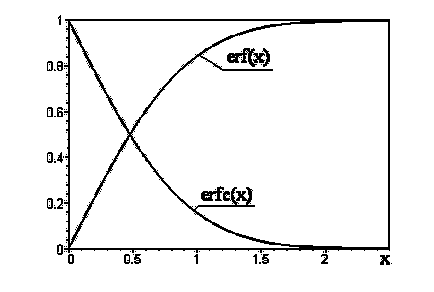
От дефиницията (3.3.3), че ЕБФ (0) = 0 и ЕБФ () = 1, т.е. ЕБФ (х) - е мога-бут-тон-но нарастваща функция да видите рояк изо-припой на Фигура 3.3. Функция ERF (х) та-бу-ли - Po-Уан и неговият znĂ-cheniya къмпинг толеранс от време в Lich неправителствени справочници; Таблица 3.1 на остров де ни няколко стойности на тази функция. Лигавника-ли-о-те-Ка не до toryh езици за програмиране-ТА са на а-ции в рамките на про-грам за вас ние-Num-среда функция ERF (х). Ако се подготвят про - грама, ние нямаме, ERF (х) функция може да си ти-Num-отливка с помощта на серия власт. "Mill-подарък-трет-Ing" веднъж-ло-напрежение ЛИЗАЦИЯ на тази функция в STE-писалка солна номер, който обикновено се съдържа в математически-Чес-кал Spra-Voch-тори, имащ form-:
E
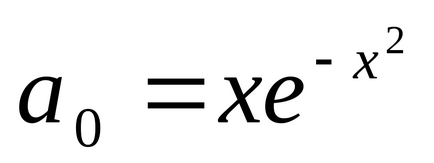
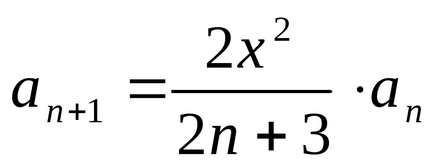
този брой възлизат лесно усукване-програма vychisleniyaerf (х) на LU-BOM език програма-E нето и га е програмиран микро-Kal-ку ла тор. Сумиране необходимо предварително край Schat, ко-GDS чрез добавяне Oche-ед-но-ти мандат на сума в размер на спирките ме-nyatsya (за да бъдат предварително Stig-ну-та "ma-гума-ценен точност").
Ако се изисква по-голяма точност, можете да използвате приблизителната коефициенти-муле:
Формула (3.3.6) дава стойностите, абсолютната грешка от които не повече от 6.310 -3. и otno-B Тел-ценен грешка на не повече от 0,71%.
Понякога, в отрицателната гама е необходимо да се определи ERF (х) х. Формула (3.3.3), е очевидно, че ЕБФ (-x) = - ЕБФ (х).
Имайте предвид, че въпреки че ЕБФ на функция (х) не е "елементарен", от гледна точка на оглед-ТА на неговите свойства и методи вас Num-среда е по-лесно, отколкото повечето "основни" функции, като например тригонометрията.
От ЕБФ на функция (х) е свързано с няколко функции, общи за топлина-Fi комуникация-постигайки кал проблеми. Това е преди всичко допълнително неразделна VE-ро-Ят-ност:
който се среща толкова често, че специална нотация се използва за него: ERFC (х) (съкращение да се чете "erfik"). Формата на тази функция също е показана на Фигура 3.3.
Много често, ЕБФ функция (х) трябва да бъдат диференцирани и в тези-grirovat. На ОП-ре-де-мент (3.3.3) следва, че
и интеграла на ERFC (х) (означен като ierfc (х)) е равен на:
Връщайки се към формула (3.3.2). Отбелязва, че ca = . можем да запишем тази формула като:
Когато т стойност функция
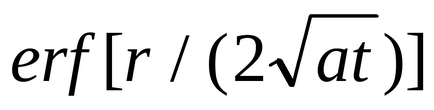
Таблица 3.1. Някои стойности на ЕБФ функция (х).