барометричното формула
В този раздел, ние се получи зависимостта на налягането на газа \ на (P \) на височината на \ (з \) над морското равнище в гравитационното поле на Земята.
Да разгледаме колона произволно цилиндрична газ напречно сечение \ (S \) и височина \ (ч. \) Тегло избран обем на газ ще бъде равна на \ [F = мг = \ р GV = \ р GHS \], където \ (\ р \) означава плътност на газа. Плътността на газ се изразява със следната формула: \ [\ изисква P = \ Frac = \ Frac >>> = \ р GH. \] Сега си такава колона в атмосферата и се изолират в него тънък слой височина въздух \ (DH \) (Фигура \ (1 \)). Ясно е, че такъв слой води до промяна в налягането със сума \ [DP = -. \ Rho GDH \] Зададохме тук знак минус, тъй като налягането трябва да се намали с увеличаването на височината.
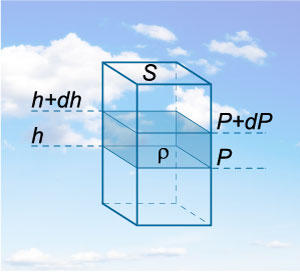
= - \ Frac >> DH> \] Като резултат, ние получаваме на диференциално уравнение описва налягането на газ \ (Р \) като височина функция \ Резултатите от интеграция в следната формула: \ [> (ч \.).
> = - \ Int >> DH>,> \; \; >> Н + \ LN С> \] изхвърляне на логаритми, ние откриваме, т.нар барометричното формула \ [P = C \ ехр \ наляво ( <- \frac>.> H> \ дясно) \] Постоянно \ (С \) се определя от първоначалното състояние \ (Р \ наляво (\ дясно) = \), където \ (\) - е средната височина барометрично налягане.
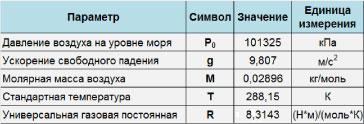
Така атмосферно зависимостта на налягането на височина, определена с формулата: ляво \ [P = \ ехр \ ( <- \frac>> H> \ дясно). \] Заместването на известните стандартни стойности (виж фигура \ (2 \) по-горе), ние откриваме \ на (Р \ ляво (ч \ дясно) \) (в килопаскала), който е описан от формула \ [>> з> \ дясно)> = \ вдясно) \; \ наляво [\ текст \ прав]> \], където височината \ (\ ч) над морското равнище, изразена в метри.Ако налягането се определя в милиметри живачен стълб \ (\ наляво (\ текст \ полето), \) формула барометричното става: \ [P \ наляво (ч \ дясно) = 760 \ ехр \ наляво ( <- 0.00012\,h> \ Десен) \ ;. \ Left [\ текст \ прав] \] барометрично формула се използва широко за оценка на атмосферното налягане при различни условия, въпреки че дава малко по-високи стойности.
Определяне на височината, на която налягането на въздуха е два пъти по-ниска от на морското равнище?
За оценка на използването на атмосферното височина формула: \ [P \ наляво (ч \ дясно) = \ ехр \ наляво ( <- 0.00012\,h> \ Дясно). \] Когато \ (H = 0 \) налягане \ (Р \ наляво (ч \ дясно) \) е средно атмосферно налягане на морското равнище \ (. \) На определена височина \ (Н \) налягане ще два пъти по-малко: \ [P \ лявата (H \ дясно) = \ Frac >> = \ ехр \ наляво ( <- 0.00012\,H> \ Десен). \] От това следва, че [\ Годен \ ляво \ ( <- 0.00012\,H> . \ Десен) = \ Frac \] Като логаритъма на двете страни, може да се намери на височината на \ (H: \) \ [= - 0.00012 \ Н,> \; \; \; \; >> \ около 5780 \, \ текст> \].Намери налягането на въздуха в мината на дълбочина \ (1 \, \ текст \) при температура \ (40 \) градуса по Целзий.
Налягането на въздуха в мината може да се оцени като се използва общата формула атмосферното. \ [P = \ ехр \ наляво ( <- \frac>.> H> \ дясно) \] Заместването в това уравнение следните стойности: \ (з = - 1000 \, \ текст \) (знак минус съответства на позицията под морското равнище), \ (Т = 40 + 273.15 = 313.15 \ \ . текстови \) останалите параметри са стандарт: \ (М = 0.02896 \, \ голям \ Frac >> \ normalsize \) \ (R = 8.3143 \, \ голям \ Frac \ cdot \ текст> \ cdot \ текст> \ normalsize \) \ (г = 9.807 \, \ голям \ Frac> ^ 2> \ normalsize. \) След прости изчисления откриваме: \ [> H> \ дясно)> = \ ехр \ наляво [ <- \frac>> \ Left ( <- 1000> \ Десен)> \ прав]> \ ок \ Годен \ ляво (\ дясно)> \ ок> \] Тъй като атмосферното налягане на морското равнище е \ (= 760 \ ;. \ Текст, \) налягането на въздуха в шахтата ще бъде равна на \ (848 \; \ текстови, \), което е приблизително \ (12 \% \) по-горе стандарт налягане на морското равнище.