монотонни функции

Определяне на увеличаване и намаляване на функция

Нека \ (у = F \ наляво (х \ дясно) \) е диференцируема функция на интервал \ на (\ наляво (\ дясно). \) Функция се нарича увеличаване на (или не-намаляване) в даден интервал, ако за всички точки \ (\ в \ наляво (\ полето), \), така че \ (0, \), така че \ [\ forall \ х \ в \ оставя (- \ делта,> \ дясно) \ стрелкаНадясно е \ наляво (х \ дясно) е \ наляво (> \ дясно). \] по същия начин се определя строго намаляване функция \ (у = F \ наляво (х \ дясно) \) в точка \ (. \)

Критерият за увеличаване и намаляване функция

Разгледа отново функция \ (у = F \ наляво (х \ полето), \) поема диференцируема в интервал \ на (\ наляво (\ дясно). \) Увеличаване или намаляване на функцията на интервал се определя от знака на първата производна функция.

Теорема 1.
За да функционира \ (у = F \ наляво (х \ дясно) \) се увеличава в интервал \ на (\ наляво (\ полето), \) е необходима и достатъчна, че първата производна на функцията е неотрицателно навсякъде в рамките на този диапазон: \ [F '\ наляво (х \ дясно) \ GE 0 \; \ forall \ х \ в \ наляво (\ дясно) \.] Същият критерий е валидна за случай на функция, намаляване интервал \ на (\ наляво (\ дясно): \) \ [г '\ наляво (х \ дясно) \ ле 0 \; \ forall \ ;. х \ в \ наляво (\ дясно) \] Ние докаже теоремата двете части (необходими и достатъчни) за случая на нарастваща функция.

Необходимо условие.
Да разгледаме произволна точка \ (\ в \ наляво (\ дясно). \) Ако (= F \ оставя у (х \ дясно) \) на функция \ увеличава с \ (\ наляво (\ полето), \) след това, по дефиниция могат да бъдат написани че \ [\ forall \ х \ в \ наляво (\ дясно): х> \ стрелкаНадясно е \ наляво (х \ дясно)> е \ наляво (> \ дясно); \] \ [\ forall \ х \ в \ наляво (\ дясно): х 0 \) навсякъде в интервал \ на (\ наляво (\ полето), \), с изключение може би само някои избрани точки, в които \ (е '\ наляво (х \ дясно) = 0, \ ) след това функция \ (е \ лявата (х \ дясно) \) е строго половина.

Съответно, състояние \ (е '\ наляво (х \ дясно) 0 \), след това функция \ (е \ ляво (х \ дясно) \) строго увеличаване в точка \ (\);

Ако \ (е '\ наляво (> \ дясно) 0 \) и \ (+ >> 0 \) (като не-отрицателни стойности \ х \ () се считат за състоянието). Резултатът е: \ [-> \ дясно) \ наляво (+> \ дясно)> 0,> \; \;> \ дясно) - е \ наляво (> \ дясно)> 0.> \] Това означава, че за да се определи тази функция \ (е \ ляво (х \ дясно) = + 1 \) се строго нараства с предварително определен интервал.

Намерете всички стойности \ (A \), за които уравнението \ (- 6 + 9x + а = 0 \) има три различни реални корени.

Кубична функция е дефинирана и диференцируема върху цялата реална линия. Негово производно се прилага чрез \ [- 6 + 9х + A> \ дясно) ^ \ нулевия >> = - 12x + 9.> \] Като се равнява на производно на нула, ние определяме функция монотонност интервали (Фигура \ (15 \)): \ [\ ; \; - 12x + 9 = 0> \; \; - 4x + 3 = 0,> \; \; = 1 \; = 3> \]

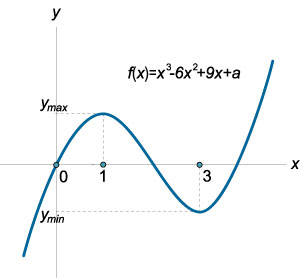
Така че преходът (от ляво на дясно) чрез точка \ (х = 1 \) увеличение на функцията се заменя със своя спад, т.е. \ (X = 1 \) е точката на максимална функция. По същия начин, \ (х = 3 \) е минималната точка на функцията. На кубичен уравнението ще има три различни реални корени в случая е показано на фигурата \ (16 \). Максимална функция трябва да вземе положителна стойност, а минимумът - е отрицателно. Така стигаме до следното условие: \ [\ ляво \<\begin y\left( 1 \right)> 0 \\ г \ ляв (3 \ дясно) 0 \\ г \ ляв (3 \ дясно) 0 \\ а - 4 \\ на 0. \) решаване на това неравенство, ние получаваме: \ [> \ cdot >> 0, > \; \; \ Десен) \ ляво (\ дясно)> 0,> \; \; -> 0,> \; \; >> \; \; 16.> \]